La media móvil de los nuevos fallecimientos diarios en España refleja, de un vistazo, el indicio halagüeño de que el país está, poco a poco, domando la pandemia :
Se da un descenso sostenido promedio de los fallecimientos diarios de un -2,4%. Sin embargo, desagregando los datos por comunidades autónomas, se observa una disparidad que me ha resultado llamativa :
A excepción de Navarra, que es densamente poco poblada, observamos que las otras tres son la más densamente poblada (Madrid), la 3ª (Canarias) y la 5ª (Cataluña). A igualdad de condiciones, me resultaría contraintuitivo que la pandemia tenga visos de resolverse más rápido en las zonas más densamente pobladas que en las menos densamente pobladas.
La prevalencia de la enfermedad 5 días después del inicio de la entrada en vigor del primer estado de alarma, el número de fallecidos por cada 100.000 habitantes fue muy dispar entre comunidades autónomas y fue, en buena medida, fruto de una “mala suerte inicial”. Sin embargo, podemos observar cómo esta mala fortuna de inicio no parece jugar ya un papel demasiado relevante a nivel de comunidades autónomas :
Podríamos poner 4 ejemplos :
Canarias NO tuvo mucha mala suerte inicial y su tendencia es DESCENDENTE.
Madrid TUVO mala suerte inicial y su tendencia es DESCENDENTE.
Murcia NO tuvo mala suerte inicial y su tendencia es ASCENDENTE.
La Rioja TUVO mala suerte inicial y su tendencia es ASCENDENTE.
Elegí trabajar con la densidad de población buscando algún indicio a favor de las zonas poco densamente pobladas, a fin de proponer empezar un plan de desescalada del confinamiento en alguna de esas zonas. Sin embargo, observar que las cifras de fallecimientos han entrado en una fase de descenso mucho más rápidamente en la mayoría de zonas más pobladas que en las menos pobladas (con independencia de las condiciones iniciales) supone para mí un indicio de que, tal vez, el confinamiento no se esté cumpliendo de igual manera en las zonas rurales que en las zonas urbanas.
Lo primero que me debo preguntar es si el Ministerio del Interior ha elaborado algún tipo de indicador del cual se pueda inferir alguna conclusión en relación a este indicio. Tal vez se me esté escapando alguna otra explicación razonable al fenómeno observado. Si no fuera así y tampoco existiera el mencionado indicador, sugiero que se investigue más en profundidad el indicio que aquí señalo.
Martín Alonso Orgaz. Carabanchel, Madrid 1987. Matemático. Ciudadano 15M, democracia, internacionalismo. Cantautor a ratos.
martes, abril 14, 2020
jueves, abril 09, 2020
¿Dónde empezar a relajar las medidas de confinamiento?
El domingo 26 de abril finaliza la vigencia del tercer Estado de Alarma decretado para abordar la crisis del COVID-19. Para tal fecha se habrán completado ya 6 semanas de confinamiento en toda España y los datos reportados diariamente reflejarán que la reclusión generalizada habrá dado sus frutos. De eso no cabe la menor duda, ahora bien, ¿habrá sido suficiente? A todas luces, no. Todos los gobiernos que han decretado el confinamiento de su población se están haciendo la misma pregunta, ¿cuál es la mejor manera de desescalar esta situación? La respuesta entraña una tremenda complejidad, al estar en juego la vida, la subsistencia y la salud física y mental de millones personas.
Cualquier colaboración entre estados es poca a la hora de afrontar la toma de decisiones durante cada una de las distintas fases de la pandemia. Para algunas cuestiones técnicas, España podrá seguir la estela de aquellos países asiáticos que están demostrando buena gestión de la crisis. Pero, lamentablemente, no basta con “copiar y pegar”. Las características socio-económicas, administrativas y demográficas de las distintas zonas afectadas hacen que cada país tenga su propio desafío. España ha sido el segundo país occidental en el que el COVID-19 ha explotado, siendo el retraso con respecto a la situación italiana de apenas pocos días. El desarrollo de acontecimientos con poco tiempo de diferencia en países semejantes al nuestro, a veces es suficiente para anticiparse y tomar medidas necesarias. No siempre.
Sea como fuere, al Gobierno no le va a quedar más remedio que ir modulando la desescalada sobre la marcha, con la dificultad añadida de que en una crisis de estas características las decisiones que hoy se tomen no tendrán un reflejo sustancial en los datos hasta dentro de varias semanas. Lo que sugeriré al Gobierno en este escrito es que elabore un plan de desescalada muy estricto, con tiempo tasado y circunscrito a un solo territorio: aquel que tenga el menor riesgo de repunte en las dos semanas siguientes. El Gobierno, en una decisión colegiada con cada una de las administraciones locales y autonómica, desarrollaría un plan piloto de desescalada del confinamiento entre los días 27 de abril y 10 de mayo que, de funcionar, empezaría a implementarse progresivamente también en otras regiones a partir del día 11 de mayo.
Modelo clásico SIR de Kermack and McKendrick
He utilizado los datos proporcionados por el Ministerio de Sanidad [1] para modelar la evolución de la pandemia en 4 comunidades autónomas españolas (Madrid, Andalucía, Murcia y Canarias) a fin de comparar, bajo las mismas hipótesis, cómo se comportaría la enfermedad en cada una de estas regiones tras una fase sin confinamiento durante las citadas fechas: las dos semanas que siguen a la finalización de la vigencia del tercer Estado de Alarma. Para ello, me he servido de las ecuaciones diferenciales del modelo SIR de Kermack and McKendrick (1927) [2], con las tasas de transmisión y de recuperación variables en el tiempo y adaptando las ecuaciones a diferencias finitas (la unidad de tiempo para la cual disponemos de datos actualizados son días, de modo que cada t será un sucesivo número entero).
donde
S(t) representa la cantidad de individuos susceptibles de ser contagiados en cierto día t.
I(t) representa la cantidad de casos activos durante el día t.
R(t) representa la suma de los pacientes que se han curado de la enfermedad y los que han fallecido para cierto día t.
β(t) representa la tasa de transmisión dinámica en cierto día t.
γ(t) representa la tasa de recuperación dinámica en cierto día t.
N, representa la población total.
Tomaremos como t = 0 la fecha del 07/03/2020, primer día para el que el Ministerio de Sanidad ofrece datos de pacientes curados. Construimos una tabla con los datos relativos a pacientes curados, casos activos y fallecimientos, desde t = 0 hasta t = 32 (08/04/2020, última fecha para la cual hay datos disponibles en la página del Ministerio de Sanidad en el momento de generar este texto), así como las cantidades calculadas con las operaciones descritas de 1) a 6), para cada t. Como ya hemos adelantado, sólo podremos obtener γ (t) y β (t) para la penúltima fecha, es decir t = 31.
Hasta aquí, lo único que hemos hecho es reproducir los datos proporcionados por el ministerio de Sanidad y calcular, para cada t = 0, …, 31, una serie de cantidades dependientes de tales datos. A continuación, utilizaremos la 2ª y la 3ª ecuación de Kermack and McKendrick para estimar, respectivamente, I(t) y R(t) para t > 32..
Utilización de medias móviles
Necesitaremos estimar unos γ y β adecuados. Para ello, nos valdremos de medias móviles de cantidades ya obtenidas de γ(t) y β(t) :
Justificación para β(t) : el cálculo directo de β(t) es demasiado sensible a fluctuaciones o retrasos en la notificación en los datos proporcionados por el Ministerio de Sanidad, de modo que tiene sentido suavizar la trayectoria de β(t) y tiene sentido hacerlo de 7 en 7 : tales retrasos vienen fuertemente condicionados por el hecho de que los datos se reflejen retrasos del fin de semana o no. Ahora bien, tomando la media móvil de solo una semana, no logré estabilizar la curva para las mencionadas proyecciones de β(t) más allá de t = 24. Tomando dos semanas, la trayectoria se volvía mucho más estable : y tiene sentido pensar que, durante las semanas de confinamiento tal trayectoria se vuelva más estable.
Justificación para γ(t) : en un primer momento, había tomado esta función constante. De hecho, el resultado no cambia mucho para la Comunidad de Madrid. Pero al trabajar con los datos de Andalucía, Murcia y Canarias observé que entre los días 03/04/2020 y 07/04/2020 aparecía una clara tendencia ascendente que no podía pasar por alto en la modelización. Por simplicidad, implementé el mismo artefacto que para β(t) : media móvil para 14 días y estimación de la futura pendiente de la trayectoria a partir de la media de las pendientes de esas medias móviles los 7 últimos días. Además, me ha parecido razonable pensar que la tasa de recuperación converja a una constante para todas las regiones. He fijado γ = 0,1041 para las 4 regiones a partir de 17/04/2020, que es la media para Madrid entre el 19/03/2020 y el 02/04/2020, fechas para las cuales he observado bastante estabilidad en esta tasa.
Proyección del modelo
Una vez que hemos calculado la prolongación de las trayectorias de las medias móviles de γ(t) y β(t) más allá de t = 24, estamos en disposición de estimar I(t) y R(t) para t > 32. Lo haremos resolviendo las ecuaciones 2ª y 3ª en sendas columnas nuevas de nuestra tabla. Los respectivos predecesores I(t-1) y R(t-1) los tomaremos de la columna que ya hemos generado en base a los datos del Ministerio de Sanidad, siempre y cuando dispongamos de tales datos. Cuando, a partir de t > 33 ya dejemos de disponer de ellos, tomaremos el dato generado por el propio modelo. Iteramos hasta t = 50, esto es, el 26/04/2020, fin de la vigencia del tercer decreto de Estado de Alarma. Por otra parte, entre t = 32 y t = 50 hemos de copiar, en las columnas reservadas para γ(t) y β(t), el resultado obtenido de las medias móviles para cada uno de esos t : utilizaremos tales estimaciones para suavizar las curvas γ(t) y β(t) que generaremos a partir de 27/04/2020 (que veremos más adelante).
Según el modelo aquí desarrollado, para tal fecha, no estaremos en condiciones de terminar con el confinamiento, la cantidad de contagiados será aún alta y decretar medidas de aislamiento para únicamente los casos activos de toda España y sus posibles contactos se antoja por completo fuera de nuestras posibilidades. La foto fija del modelo para el 26/04/2020 señala que, en particular, en estas 4 comunidades autónomas, habrá la siguiente cantidad de casos activos :

Ahora bien, dado que la evolución de la pandemia en España lleva un curso desigual en función de diversos factores, también geográficos, podría ser una buena idea averiguar qué regiones son menos susceptibles de sufrir repuntes importantes a partir del 27/04/2020 para desarrollar un plan piloto de desescalada del confinamiento, ampliable a otras zonas (en función de los resultados) a partir del 11/05/2020. Para dar con la mejor respuesta, evidentemente, no basta con esta modelización matemática, habrá que tener en cuenta otros factores como la capacidad asistencial del sistema sanitario en la zona finalmente elegida.
Hablando en términos del modelo, no es ni necesario ni suficiente que la tasa de transmisión β llegue a casi 0 para evitar un repunte de los contagios. De nada serviría estar totalmente confinados, lograr ese β ≈ 0 en el modelo, que el país vuelva totalmente a su actividad normal y que unos pocos casos sin controlar pudieran reproducir de nuevo los acontecimientos en los que estamos ahora inmersos. Más valdría, sobre todo en esta primera etapa de desescalada, mantener en el tiempo una tasa de transmisión β < 0,1 (esto implicaría un descenso sostenido de los casos activos) mediante un plan de “vuelta a la normalidad” muy prudente que no nos llevara a dar pasos en falso con fatales consecuencias. Conseguir ese β < 0,1 depende de muchos factores, que esta modelización no pretende abarcar.
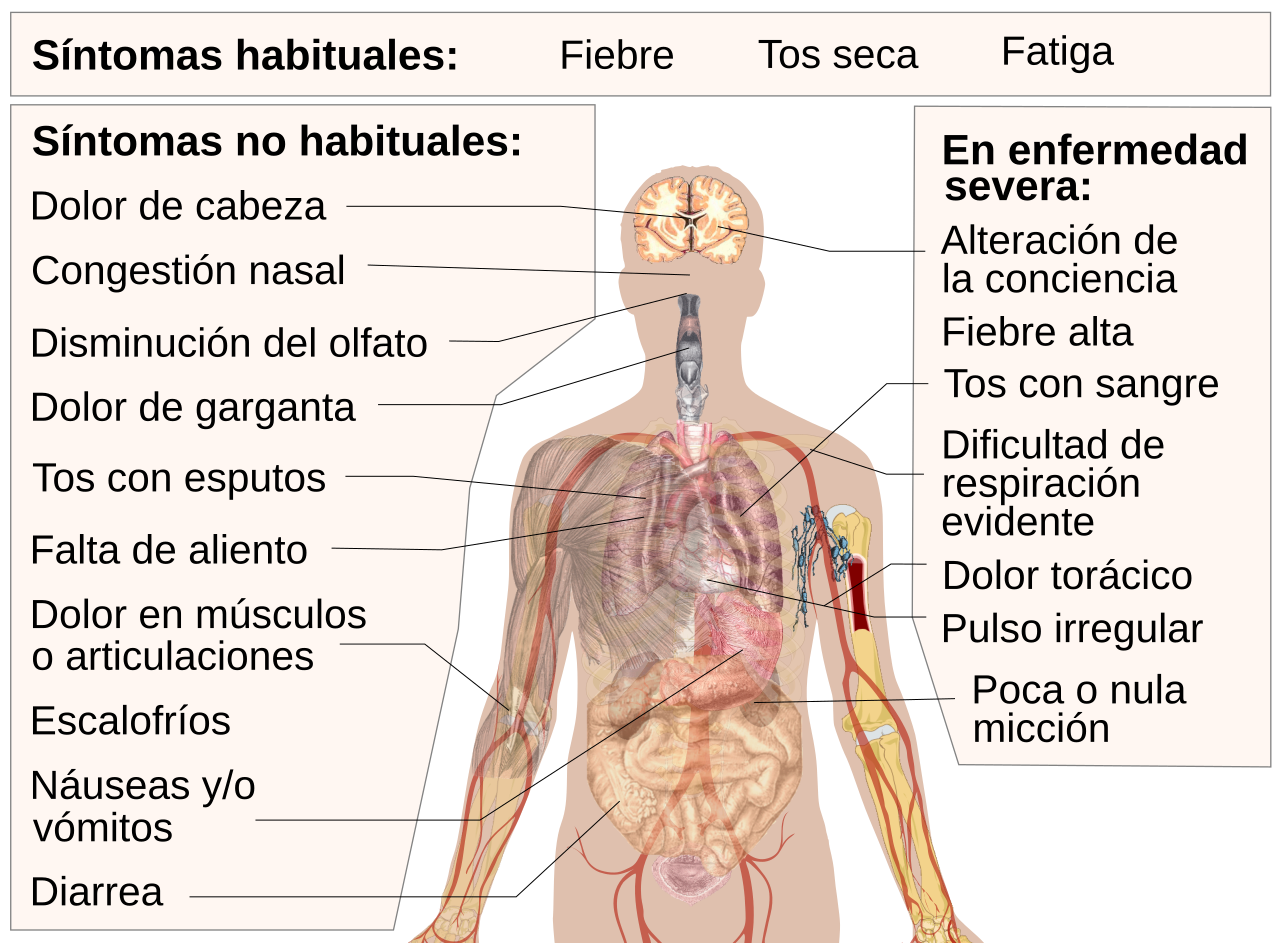
Valga la siguiente comparación entre las 4 comunidades autónomas elegidas para hacernos una idea del grado de magnitud del peligro de trazar un plan de desescalada demasiado a la ligera. Para ello, me serviré de la tasa de transmisión dinámica calculada a través de los datos del Ministerio de Sanidad.para el día 19/03/2020 y días cercanos en cada una de estas 4 regiones. La elección de ese día responde a que estoy estimando en 5 los días que transcurren desde que una persona contagiada puede contagiar a la siguiente. Esto no es exactamente así: lo que se estima en 5,1 días es el tiempo que transcurre desde que una persona contagiada desarrolla síntomas (según un estudio de la Universidad John Hopkins). Para que tales cantidades coincidieran serían necesarias dos cosas: que el momento de desarrollar síntomas sea el de más probable contagio y que cada persona contagiara únicamente a otra. Aún así, escoger un decalaje de 5 días me ha parecido lo más adecuado. Y el 19/03/2020 es 5 días después del 14/03/2020, momento justo anterior al confinamiento. Como los datos fluctúan, resulta conveniente considerar una media que incluya los 3 días siguientes y los 3 días precedentes :
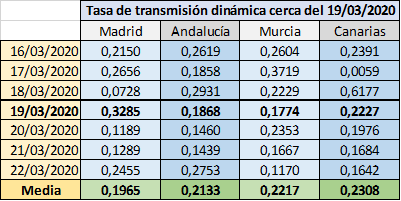
Haremos uso de estos datos para modelar una situación de no confinamiento entre el 26/04/2020 y el 10/05/2020 que da lugar a un arrepentimiento ejecutivo tal que el 11/05/2020 el Gobierno vuelve a decretar un confinamiento con las mismas características que las actuales. Aplicando el señalado decalaje de 5 días, supondremos que entre el 02/05/2020 y el 15/05/2020 hubiese una tasa de transmisión dinámica equivalente a la estimada, en cada región, el 19/03/2020. Haremos ajustes con medias móviles y medias de diferencias finitas para suavizar la trayectoria en los días anteriores y en los siguientes.
Justificación : trasladar, sin más, una tasa de transmisión dinámica de una fecha a otra no nos va a generar resultados numéricamente cercanos a la realidad (si es que esa realidad se produjese). Sin embargo, juzgo útil hacer este ejercicio porque ayuda a modelar una misma situación, bajo las mismas hipótesis, para diferentes regiones: lo útil no serán los resultados numéricos, sino la comparación de los órdenes de magnitud entre las diferentes regiones, y entre dos las curvas generadas en cada región.




Desde, aproximadamente esta semana hasta la última semana de abril, la cantidad de casos activos no dejará de bajar. Si dejamos el confinamiento demasiado rápido, la cantidad de casos activos volverá a subir a principios de mayo y habrá que revertir la decisión. Ahora bien, observamos que el efecto no es el mismo en cada una de las regiones. Por un lado, no pasemos por alto el eje de ordenadas : cada gráfica tiene su propio orden de magnitud. Por otro lado, observamos que la magnitud de la segunda curva es también diferente con respecto de la primera al comparar entre gráficas. Y, en especial, observamos que en Canarias la diferencia entre ambas curvas es más que notable.
Conclusión
Elegí Madrid, por un lado y Andalucía, Murcia y Canarias, por otro, al ser, respectivamente, la comunidad autónoma con mayor incidencia de COVID-19 y las tres regiones con menor incidencia. Si hubiera que elegir una de estas 4 Comunidades Autónomas para comenzar una desescalada del confinamiento, sería Canarias. Pero creo que sería útil aplicar un modelado de este tipo de una manera más pormenorizada a algunas regiones en particular, ya sean provincias, islas, comarcas, municipios o entidades de otra naturaleza. Regiones que el Gobierno, demás administraciones y organismos técnicos y de gestión sanitaria, todos coordinados, consideren posible comenzar un plan piloto de desescalada del confinamiento. Dadas las particularidades socio-económicas, administrativas, demográficas y de recursos sanitarios disponibles, deben ser las autoridades las que determinen las entidades geográficas candidatas a desarrollar el plan piloto sugerido.
Bibliografía y recursos
[1] Situación de COVID-19 o Coronavirus en España - Ministerio de Sanidad
[2] Ajuste de los datos oficiales del COVID-19 mediante un modelo SIR con tasa de transmisión dinámica - José E. Chacón - Universidad de Extremadura
Datos de contacto : alonsorgaz(arroba)gmail(punto)com
Cualquier colaboración entre estados es poca a la hora de afrontar la toma de decisiones durante cada una de las distintas fases de la pandemia. Para algunas cuestiones técnicas, España podrá seguir la estela de aquellos países asiáticos que están demostrando buena gestión de la crisis. Pero, lamentablemente, no basta con “copiar y pegar”. Las características socio-económicas, administrativas y demográficas de las distintas zonas afectadas hacen que cada país tenga su propio desafío. España ha sido el segundo país occidental en el que el COVID-19 ha explotado, siendo el retraso con respecto a la situación italiana de apenas pocos días. El desarrollo de acontecimientos con poco tiempo de diferencia en países semejantes al nuestro, a veces es suficiente para anticiparse y tomar medidas necesarias. No siempre.
Sea como fuere, al Gobierno no le va a quedar más remedio que ir modulando la desescalada sobre la marcha, con la dificultad añadida de que en una crisis de estas características las decisiones que hoy se tomen no tendrán un reflejo sustancial en los datos hasta dentro de varias semanas. Lo que sugeriré al Gobierno en este escrito es que elabore un plan de desescalada muy estricto, con tiempo tasado y circunscrito a un solo territorio: aquel que tenga el menor riesgo de repunte en las dos semanas siguientes. El Gobierno, en una decisión colegiada con cada una de las administraciones locales y autonómica, desarrollaría un plan piloto de desescalada del confinamiento entre los días 27 de abril y 10 de mayo que, de funcionar, empezaría a implementarse progresivamente también en otras regiones a partir del día 11 de mayo.
Modelo clásico SIR de Kermack and McKendrick
He utilizado los datos proporcionados por el Ministerio de Sanidad [1] para modelar la evolución de la pandemia en 4 comunidades autónomas españolas (Madrid, Andalucía, Murcia y Canarias) a fin de comparar, bajo las mismas hipótesis, cómo se comportaría la enfermedad en cada una de estas regiones tras una fase sin confinamiento durante las citadas fechas: las dos semanas que siguen a la finalización de la vigencia del tercer Estado de Alarma. Para ello, me he servido de las ecuaciones diferenciales del modelo SIR de Kermack and McKendrick (1927) [2], con las tasas de transmisión y de recuperación variables en el tiempo y adaptando las ecuaciones a diferencias finitas (la unidad de tiempo para la cual disponemos de datos actualizados son días, de modo que cada t será un sucesivo número entero).
S(t + 1) = S(t) − β(t) S(t) I(t) / N,
I(t + 1) = I(t) + β(t) S(t) I(t) / N − γ(t) I(t),
R(t + 1) = R(t) + γ(t) I(t)
donde
S(t) representa la cantidad de individuos susceptibles de ser contagiados en cierto día t.
I(t) representa la cantidad de casos activos durante el día t.
R(t) representa la suma de los pacientes que se han curado de la enfermedad y los que han fallecido para cierto día t.
β(t) representa la tasa de transmisión dinámica en cierto día t.
γ(t) representa la tasa de recuperación dinámica en cierto día t.
N, representa la población total.
- En primer lugar calculamos R(t) tomando los datos del Ministerio de Sanidad para los pacientes curados y los fallecidos para cada día t.
- Después calculamos I(t), restando, al total de casos confirmados por el Ministerio de Sanidad para cada día t, el correspondiente R(t), ya calculado.
- Para obtener γ(t), hacemos uso de la 3ª ecuación. Este dato lo obtendremos con un día de retraso, al necesitar, para cada t, de R(t + 1). Entonces, podremos resolver :γ(t) = (R(t + 1) - R(t)) / I(t).
- Tomamos como N, el dato disponible más actualizado posible: el proporcionado por el INE para cada comunidad autónoma en 2019.
- Por simplicidad, calculamos S(t) bajo la hipótesis de que no hubiese personas inmunizadas que el sistema sanitario hubiese pasado por alto. Esto es, simplemente restamos a la población total, N, la cantidad de casos activos, curados y fallecidos, esto es :S(t) = N - I(t) - R(t)
- Finalmente, despejamos β(t) de la 2ª ecuación. Este dato también lo obtendremos con un día de retraso, al necesitar, para cada t, de I(t + 1). Entonces, podremos resolver :β(t) = ((I(t + 1) + (γ(t) - 1) I(t)) N) / (S(t) I(t))
Tomaremos como t = 0 la fecha del 07/03/2020, primer día para el que el Ministerio de Sanidad ofrece datos de pacientes curados. Construimos una tabla con los datos relativos a pacientes curados, casos activos y fallecimientos, desde t = 0 hasta t = 32 (08/04/2020, última fecha para la cual hay datos disponibles en la página del Ministerio de Sanidad en el momento de generar este texto), así como las cantidades calculadas con las operaciones descritas de 1) a 6), para cada t. Como ya hemos adelantado, sólo podremos obtener γ (t) y β (t) para la penúltima fecha, es decir t = 31.
Hasta aquí, lo único que hemos hecho es reproducir los datos proporcionados por el ministerio de Sanidad y calcular, para cada t = 0, …, 31, una serie de cantidades dependientes de tales datos. A continuación, utilizaremos la 2ª y la 3ª ecuación de Kermack and McKendrick para estimar, respectivamente, I(t) y R(t) para t > 32..
Utilización de medias móviles
Necesitaremos estimar unos γ y β adecuados. Para ello, nos valdremos de medias móviles de cantidades ya obtenidas de γ(t) y β(t) :
- A partir de t = 5, calculamos las medias móviles de γ(t) y de β(t), haciendo uso de las respectivas cantidades para t ∈ [t - 5 ; t + 8], es decir, para cada t, abarcamos un total de 14 días, empezando 5 días antes y terminando 8 días después (ambos inclusive). Aplicando este criterio, sólo podremos calcular estas medias móviles con datos reales hasta t = 31 - 8 = 23.
- Por otra parte, para cada una de las 7 últimas medias móviles calculamos la diferencia finita con respecto a su predecesora. Según vayamos iterando, incorporaremos cada media generada en el cálculo de la siguiente diferencia finita.
- Calculamos la continuación de la trayectoria de las medias móviles γ(t) y β(t) más allá de t = 24 valiéndonos de la media de diferencias finitas que acabamos de calcular.
Justificación para β(t) : el cálculo directo de β(t) es demasiado sensible a fluctuaciones o retrasos en la notificación en los datos proporcionados por el Ministerio de Sanidad, de modo que tiene sentido suavizar la trayectoria de β(t) y tiene sentido hacerlo de 7 en 7 : tales retrasos vienen fuertemente condicionados por el hecho de que los datos se reflejen retrasos del fin de semana o no. Ahora bien, tomando la media móvil de solo una semana, no logré estabilizar la curva para las mencionadas proyecciones de β(t) más allá de t = 24. Tomando dos semanas, la trayectoria se volvía mucho más estable : y tiene sentido pensar que, durante las semanas de confinamiento tal trayectoria se vuelva más estable.
Justificación para γ(t) : en un primer momento, había tomado esta función constante. De hecho, el resultado no cambia mucho para la Comunidad de Madrid. Pero al trabajar con los datos de Andalucía, Murcia y Canarias observé que entre los días 03/04/2020 y 07/04/2020 aparecía una clara tendencia ascendente que no podía pasar por alto en la modelización. Por simplicidad, implementé el mismo artefacto que para β(t) : media móvil para 14 días y estimación de la futura pendiente de la trayectoria a partir de la media de las pendientes de esas medias móviles los 7 últimos días. Además, me ha parecido razonable pensar que la tasa de recuperación converja a una constante para todas las regiones. He fijado γ = 0,1041 para las 4 regiones a partir de 17/04/2020, que es la media para Madrid entre el 19/03/2020 y el 02/04/2020, fechas para las cuales he observado bastante estabilidad en esta tasa.
Proyección del modelo
Una vez que hemos calculado la prolongación de las trayectorias de las medias móviles de γ(t) y β(t) más allá de t = 24, estamos en disposición de estimar I(t) y R(t) para t > 32. Lo haremos resolviendo las ecuaciones 2ª y 3ª en sendas columnas nuevas de nuestra tabla. Los respectivos predecesores I(t-1) y R(t-1) los tomaremos de la columna que ya hemos generado en base a los datos del Ministerio de Sanidad, siempre y cuando dispongamos de tales datos. Cuando, a partir de t > 33 ya dejemos de disponer de ellos, tomaremos el dato generado por el propio modelo. Iteramos hasta t = 50, esto es, el 26/04/2020, fin de la vigencia del tercer decreto de Estado de Alarma. Por otra parte, entre t = 32 y t = 50 hemos de copiar, en las columnas reservadas para γ(t) y β(t), el resultado obtenido de las medias móviles para cada uno de esos t : utilizaremos tales estimaciones para suavizar las curvas γ(t) y β(t) que generaremos a partir de 27/04/2020 (que veremos más adelante).
Según el modelo aquí desarrollado, para tal fecha, no estaremos en condiciones de terminar con el confinamiento, la cantidad de contagiados será aún alta y decretar medidas de aislamiento para únicamente los casos activos de toda España y sus posibles contactos se antoja por completo fuera de nuestras posibilidades. La foto fija del modelo para el 26/04/2020 señala que, en particular, en estas 4 comunidades autónomas, habrá la siguiente cantidad de casos activos :
Ahora bien, dado que la evolución de la pandemia en España lleva un curso desigual en función de diversos factores, también geográficos, podría ser una buena idea averiguar qué regiones son menos susceptibles de sufrir repuntes importantes a partir del 27/04/2020 para desarrollar un plan piloto de desescalada del confinamiento, ampliable a otras zonas (en función de los resultados) a partir del 11/05/2020. Para dar con la mejor respuesta, evidentemente, no basta con esta modelización matemática, habrá que tener en cuenta otros factores como la capacidad asistencial del sistema sanitario en la zona finalmente elegida.
Hablando en términos del modelo, no es ni necesario ni suficiente que la tasa de transmisión β llegue a casi 0 para evitar un repunte de los contagios. De nada serviría estar totalmente confinados, lograr ese β ≈ 0 en el modelo, que el país vuelva totalmente a su actividad normal y que unos pocos casos sin controlar pudieran reproducir de nuevo los acontecimientos en los que estamos ahora inmersos. Más valdría, sobre todo en esta primera etapa de desescalada, mantener en el tiempo una tasa de transmisión β < 0,1 (esto implicaría un descenso sostenido de los casos activos) mediante un plan de “vuelta a la normalidad” muy prudente que no nos llevara a dar pasos en falso con fatales consecuencias. Conseguir ese β < 0,1 depende de muchos factores, que esta modelización no pretende abarcar.
Valga la siguiente comparación entre las 4 comunidades autónomas elegidas para hacernos una idea del grado de magnitud del peligro de trazar un plan de desescalada demasiado a la ligera. Para ello, me serviré de la tasa de transmisión dinámica calculada a través de los datos del Ministerio de Sanidad.para el día 19/03/2020 y días cercanos en cada una de estas 4 regiones. La elección de ese día responde a que estoy estimando en 5 los días que transcurren desde que una persona contagiada puede contagiar a la siguiente. Esto no es exactamente así: lo que se estima en 5,1 días es el tiempo que transcurre desde que una persona contagiada desarrolla síntomas (según un estudio de la Universidad John Hopkins). Para que tales cantidades coincidieran serían necesarias dos cosas: que el momento de desarrollar síntomas sea el de más probable contagio y que cada persona contagiara únicamente a otra. Aún así, escoger un decalaje de 5 días me ha parecido lo más adecuado. Y el 19/03/2020 es 5 días después del 14/03/2020, momento justo anterior al confinamiento. Como los datos fluctúan, resulta conveniente considerar una media que incluya los 3 días siguientes y los 3 días precedentes :
Haremos uso de estos datos para modelar una situación de no confinamiento entre el 26/04/2020 y el 10/05/2020 que da lugar a un arrepentimiento ejecutivo tal que el 11/05/2020 el Gobierno vuelve a decretar un confinamiento con las mismas características que las actuales. Aplicando el señalado decalaje de 5 días, supondremos que entre el 02/05/2020 y el 15/05/2020 hubiese una tasa de transmisión dinámica equivalente a la estimada, en cada región, el 19/03/2020. Haremos ajustes con medias móviles y medias de diferencias finitas para suavizar la trayectoria en los días anteriores y en los siguientes.
Justificación : trasladar, sin más, una tasa de transmisión dinámica de una fecha a otra no nos va a generar resultados numéricamente cercanos a la realidad (si es que esa realidad se produjese). Sin embargo, juzgo útil hacer este ejercicio porque ayuda a modelar una misma situación, bajo las mismas hipótesis, para diferentes regiones: lo útil no serán los resultados numéricos, sino la comparación de los órdenes de magnitud entre las diferentes regiones, y entre dos las curvas generadas en cada región.
Desde, aproximadamente esta semana hasta la última semana de abril, la cantidad de casos activos no dejará de bajar. Si dejamos el confinamiento demasiado rápido, la cantidad de casos activos volverá a subir a principios de mayo y habrá que revertir la decisión. Ahora bien, observamos que el efecto no es el mismo en cada una de las regiones. Por un lado, no pasemos por alto el eje de ordenadas : cada gráfica tiene su propio orden de magnitud. Por otro lado, observamos que la magnitud de la segunda curva es también diferente con respecto de la primera al comparar entre gráficas. Y, en especial, observamos que en Canarias la diferencia entre ambas curvas es más que notable.
Conclusión
Elegí Madrid, por un lado y Andalucía, Murcia y Canarias, por otro, al ser, respectivamente, la comunidad autónoma con mayor incidencia de COVID-19 y las tres regiones con menor incidencia. Si hubiera que elegir una de estas 4 Comunidades Autónomas para comenzar una desescalada del confinamiento, sería Canarias. Pero creo que sería útil aplicar un modelado de este tipo de una manera más pormenorizada a algunas regiones en particular, ya sean provincias, islas, comarcas, municipios o entidades de otra naturaleza. Regiones que el Gobierno, demás administraciones y organismos técnicos y de gestión sanitaria, todos coordinados, consideren posible comenzar un plan piloto de desescalada del confinamiento. Dadas las particularidades socio-económicas, administrativas, demográficas y de recursos sanitarios disponibles, deben ser las autoridades las que determinen las entidades geográficas candidatas a desarrollar el plan piloto sugerido.
Bibliografía y recursos
[1] Situación de COVID-19 o Coronavirus en España - Ministerio de Sanidad
[2] Ajuste de los datos oficiales del COVID-19 mediante un modelo SIR con tasa de transmisión dinámica - José E. Chacón - Universidad de Extremadura
Datos de contacto : alonsorgaz(arroba)gmail(punto)com
Suscribirse a:
Comentarios (Atom)




